The 1st person can choose a whatever birthday (e.g., say April
1). Then the probability that the 2nd person has the same birth day
(April 1) is ![]() .
.
Let's name the 3 people: A, B and C. The 1st person (A) can choose a
whatever birthday (e.g., say April 1). Then the probability that the
2nd person has the same birthday (April 1) is
![]() .
Similarly, the probability that the 3rd person has the same birthday
is also
.
Similarly, the probability that the 3rd person has the same birthday
is also
![]() . So we want to get the Probability that A=B
AND A=C:
. So we want to get the Probability that A=B
AND A=C:
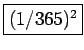 .
.
The 1st person (A) can choose a whatever birthday (e.g., April 1). B can choose any birthday other than April 1, so the probability is (365-1)/365. Let's say B's birthday is March 1. C can choose any day other than March 1 and April 1, so the probability is (365-1-1)/365.
The correct answer is
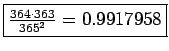 .
.
Common mistake:
![]() :
: ![]() is the probabilty that
all 3 has the same birthday. So
is the probabilty that
all 3 has the same birthday. So ![]() is the probability
that at least one person among 3 has the different birthday. This
probability include the cases where
is the probability
that at least one person among 3 has the different birthday. This
probability include the cases where ![]() ,
, ![]() ,
and
,
and ![]() .
.
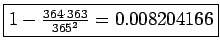 The opposite of
the previous question.
The opposite of
the previous question.
Similar idea to the previous question. First let's calculate the
probability that all 20 people has different birthday. This
probability is
![]() . So
. So
![]() is the
probability that at least one pair has the same birthday in a group of
20 people. It's a pretty high probability, isn't it?
is the
probability that at least one pair has the same birthday in a group of
20 people. It's a pretty high probability, isn't it?
To generalize this, the probability that at least one pair has the
same birthday in a group of n people is:
![]() .
.
There are
![]() elementary outcomes: (1,1), (1,2), (1,3),
(1,4), (1,5), (1,6), (2,1), (2,2), ...., (6,6). Of these elementary
outcomes , only (1,6), (2,3), (3,2) and (6,3) can give the event that
the product of these 2 values to be 6. The answer is
elementary outcomes: (1,1), (1,2), (1,3),
(1,4), (1,5), (1,6), (2,1), (2,2), ...., (6,6). Of these elementary
outcomes , only (1,6), (2,3), (3,2) and (6,3) can give the event that
the product of these 2 values to be 6. The answer is
![]() .
.
This is basically saying that 2 dice does not match.
![]()
From one roll of two dice, the probability that the two dice match is
1/6, and the probability that the two dice do not match is ![]() .
.
This problem can be handled by binominal distribution if you define that R.V. X is the number of times that 2 dice match. Then we can use n=3, and the probabilitty of success can be defined as the probability that 2 dies match: p=1/6.
![]() .
.
So the question asks the probability that X=1:
![\fbox{$Pr[X = 1] = {3 \choose 1} (1/6)^1 (5/6)^{3 - 1} = 3 \cdot
5^2/6^3 = 0.34722$}](img20.png) .
.
If the question were to obtain the probability that the two dice will
match on at least one of the three rolls we would get
![]() . An easier way to calculate
this probability is to subtract the probability that the two dice
doesn't match in any of the 3 trials from 1:
. An easier way to calculate
this probability is to subtract the probability that the two dice
doesn't match in any of the 3 trials from 1:
![]() .
.