Non-uniform random numbers

In simulations, you frequently need to generate random number following a distributions other than uniform distributions. In previous exercises, you have already created a rather simple way to draw a random number from the binominal distribution and geometric distribution (remember the coin flipping functions in the homeworks?).

Here I briefly discuss about approaches to create non-uniform random numbers from uniform PRNG.

In reality, I generally use pre-made functions from a library called GNU Scientific Library (GSL).

transformation

Easy when inverse function of cumulative distribution function can be obtained.

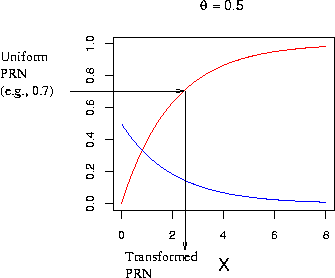
e.g., To create a random number y from exponential distribution, draw a unifrom PRN z [0,1), and use the following transformation.

$$y = - \frac{ln(z)}{\theta}$$

rejection method

Sometimes, you know the probability density/mass function, but cumulative distribution function is difficult to calculate.

• g(x): envelope function, whose shape is similar to the actual distribution (f(x)). This function should lie above f(x), and the inverse of $\int_{- \infty}^x g(x) dx$ can be calculated easily.
• Draw a first uniform PRN, and transform it with the inverse function of $\int_{- \infty}^x g(x) dx$ to create a candidate j.
• Draw a second uniform PRN between 0 and g(j).
• If the 2nd PRN is less than f(j), accept it as a PRN drawn from a distribution f(x). If not, reject it, and draw another candidate until you find an acceptable one.

Random numbers with GSL

Life is much easier if you know how to use GSL since you don't have to reinvent the wheels. GNU Scientific Library (GSL) is a collection of numerical routines for scientific computing. It's an open source project, and it can be compiled for many platforms (e.g., linux, Mac OS-X, Windows with Cygwin). You may need to install GSL before you can use it (it's usually not installed by default). Here I briefly show how to use the uniform and non-uniform random number generators implemented in GSL. There are many other useful functions, so take a look at the manual. Two sections of manual is relevant for our purpose (PRNGs and Distributions).

• Example

  #include <stdio.h>
  #include <gsl/gsl_rng.h>
  #include <gsl/gsl_randist.h>
  
  const gsl_rng *gBaseRand;       /* global rand number generator */
  
  int main (void) {
    unsigned long randSeed;
    int i, k, n = 10;
    double lambda = 3.0;
  
    /* specifying to use Mersenne twister MT-19937 as the uniform PRNG */
    gBaseRand = gsl_rng_alloc(gsl_rng_mt19937);
    
    srand(time(NULL));                    /* initialization for rand() */
    randSeed = rand();                    /* returns a non-negative integer */
    gsl_rng_set (gBaseRand, randSeed);    /* seed the PRNG */
    
    /* print n random variates chosen from  the poisson distribution with mean 
       parameter lambda */
    for (i = 0; i < n; i++) {
        k = gsl_ran_poisson (gBaseRand, lambda);
        printf (" %u", k);
      }
  
    printf ("\n");
    gsl_rng_free(gBaseRand);
    return 0;
  }
  

• Explanation of key elements:
  • You need to use the two header files
  • const gsl_rng *gBaseRand;

    Making a special global variable (I'm calling it gBaseRand), which stores what kind of uniform random number generator you want to use.

  • gBaseRand = gsl_rng_alloc(gsl_rng_mt19937);

    We are setting this variable to use gsl_rng_mt19937.
    There are many other PRNGs which you can specify (e.g., you can use the familiar drand48() if you specify gsl_rnd_rand48).

  • gsl_rng_set (gBaseRand, randSeed);

    Seeding the specified PRNG (gBaseRand) with a seed (randSeed).

  • k = gsl_ran_poisson (gBaseRand, lambda);
    

    Use gBaseRand as the base uniform PRNG, and draw a random number from a poisson distribution (whose parameter is specified as lambda).

  • gsl_rng_free(gBaseRand); Free the memory allocated for the PRNG
• Compilation (You can copy /home/progClass/src/prng/prng.c.)

  gcc prng.c -lgsl -lgslcblas -lm
  

  • -llibraryName means link with the library.
  • Linking means that extract the functions used in your source code from the library and attach them to your object code.
  • To use the random number generators, you need to link with 3 libraries: gsl, gslcblas (basic linear algebra subprograms), and m (math).

• Other useful random number functions

  The first argument for all the functions are the variable containing the type of uniform PRNG (here I'm using gBaseRand).

  • Discrete distribution
    Retuns unsigned int.
    gsl_ran_binomial (gBaseRand, double p, unsigned int n)
gsl_ran_geometric (gBaseRand, double p)
gsl_ran_negative_binomial (gBaseRand, double p, double n)
gsl_ran_poisson (gBaseRand, double lambda)
    

    Returns unsigned long int
    gsl_rng_uniform_int(gBaseRand, unisigned long int n)
        Uniform distribution, between 0 to n-1 inclusive.

  • Continuous distributions
    All returns double.

    gsl_ran_gaussian (gBaseRand, double sigma)	Normal distribution with mean of 0
    gsl_ran_exponential (gBaseRand, double theta)	Exponential distribution
    gsl_ran_flat (gBaseRand, double a, double b)	Uniform (flat) distribution, a <= x < b, [a, b)
    gsl_rng_uniform(gBaseRand)	Uniform, 0 <= x < 1, [0, 1)
    gsl_rng_uniform_pos(gBaseRand)	Uniform, 0 < x < 1, (0, 1)

There are many more distributions in GSL, and you can use them in the same way as the example above.

Exercises

• Create a program to print out the random numbers drawn from a whatever distribution implemented in GSL function. Take a look at the manual if you want to try other kinds of dstributions not listed above. Print out many random numbers (say 10000, each line contains one random number). Capture the output to a file (e.g out1.txt). Then use R to plot the distribution.

  $ R
  > dat <- read.table("out1.txt")
  > hist(dat[,1])
  > mean(dat[,1])
  > var(dat[,1])
  > q()
  

  Compare the observed mean and variance with the expectation if you are using one of the distribution we covered in the class.

  Try to use several different distributions. Also change the parameters of distributions, and observe how the shape changes.

• Model of minority cytotype exclusion in polyploidy.
  When there is a population with mixed ploidy, inter-ploidy cross can create infertile offspring. This create a competition between ploidy levels. Implement a stochastic model simulating this process, and analyze the outcome. For examples, you can analyze how the initial frequencies influence the final outcome, how time till exclusion by one ploidy is influenced by different parameter values, whether coexistence of two ploidy levels can be possible under certain parameter combinations. Or you can start from a diploid population and introduce a tetraploid individual, and see when the tetraploid individual can invade into the population.
  • t tetraploids and d diploids in a population (N = t + d), and N stays constant.
  • Each plant makes only 1 flower (like tulips). Number of ovules per flower is normally distributed with mean o and standard deviation w.
  • Proportion s of the ovules are self-fertilized (binominal distribution). The rest are fertilized by other plants (outcrossed).
  • Assume that the fitness of outcrossed and selfed seeds are the same (no inbreeding depression).
  • Number of pollinator visits per flower is the Poisson distribution with parameter v.
  • Each pollinator visit results in deposition of 100 pollen grains from the flower visitation immediately before this flower. Assuming that the polinator visit plants randomly, the probability that the previous visit was diploid is d/N.
  • If x ovules are available for outcrossing and if the flower received a diploid pollen and b tetraploid pollen, the number of ovule fertilized by diploid pollen is binominally distributed (number of trials = x and probability of success is a/(a+b).
  • For a simplicity, let's assume that triploid seeds get aborted after fertilization (not biologically realistic). In other words, the ovules used for interploidy crosses are wasted.
  • After one generation, there will be l diploid seeds, and m tetraploid seeds. To create the next generation, you can use the binominal distribution.